Islam Mohamed
A Semantic-based Method for Unsupervised Commonsense Question Answering

introduction
- Since existing methods can be easily distracted by irrelevant factors such as lexical perturbations, we argue that a commonsense question answering method should focus on the answers’ smantics and assign similar scores to synonymous choices.
Method
- In this paper, we focus on unsupervised multiple-choice commonsense question answering, which is formalized as follows: given a question and a set of choices, models should select the correct choice:
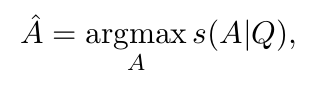
- where s refers to a score function.
- Note that we have no access to any labeled task data.
SEQA
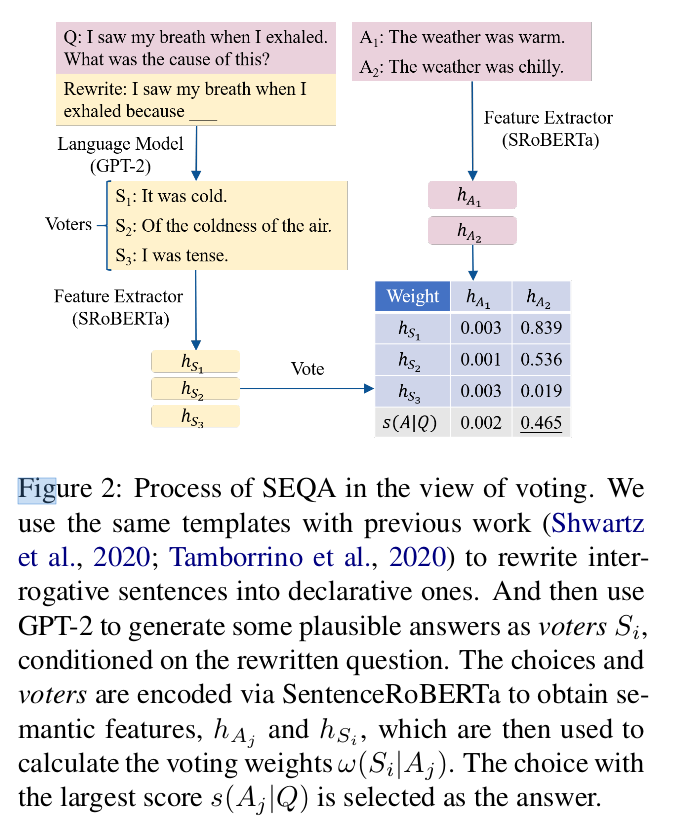
- Instead of directly estimating the probability P(A|Q) of the single choice A.
- The semantic score focuses on the probability P (M of A|Q) where M of A represents A’s semantics.
- Ideally, we decompose P(M of A |Q) into the summation of the conditional probabilities of A’s supporters, where the supporters indicates all possible answers that have exactly the same semantics M of A .
- Formally, the semantic score is defined as:
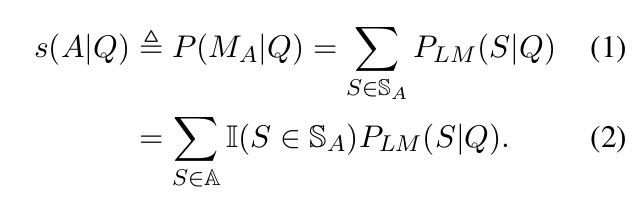
- S of A is the set of supporters of choice A, and A is the set of all possible answers.
- I(S ∈ S of A ) is an indicator function indicating whether S is a supporter of A.
- To obtain the supporter set S of A , we adopt a model to extract the sentence-level semantic features.
- Ideally, the indicator function is defined as
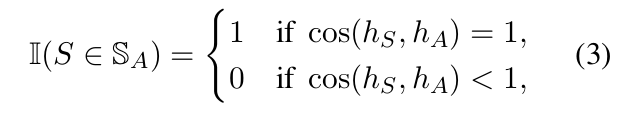
- where h of A is the semantic features of sentence A, and we assume that S and A are exactly the same in semantics if h of S and h of A point in the same direction.
- However, Eq.(3) uses a hard constraint that cos(h S , h A ) exactly equals to 1, which can be too strict to find acceptable supporters. Therefore, we reformulate Eq.(2) into a soft version:
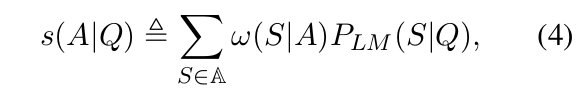
- where the indicator function in Eq.(2) is replaced by a soft function ω(S|A).
- To emulate I(S ∈ S A ), ω(S|A) is expected to meet three requirements:
- ω(S|A) ∈ [0, 1] for any S and A.
- ω(S|A) = 1 if cos(h of S , h of A ) = 1
- ω(S|A) increases monotonically with cos(h of S , h of A ).
- In this paper, ω(S|A) is defined as:
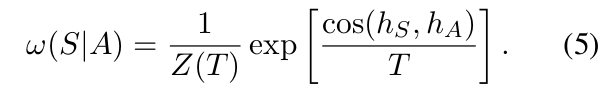
- T is the temperature, and Z(T) = exp(1/T) is a normalization term that makes ω(A|A) = 1.
- If T → 0, ω(S|A) degenerates to the indicator function.
- If T > 0, ω(S|A) relates to the von Mises-Fishers distribution over the unit sphere in the feature space, where the acceptable feature vectors are distributed around the mean direction h of a / || h of a ||
- Since it is intractable to enumerate all possible answers in A, we convert Eq.(4) to an expectation over P LM (S|Q):
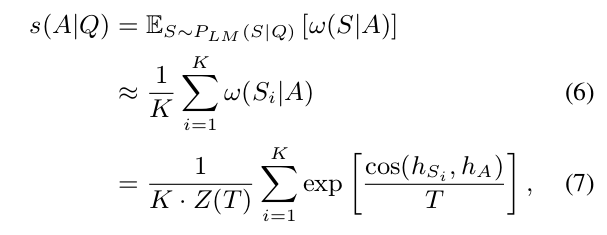
- where S1 , · · · , SK are sentences sampled from P LM (·|Q), and K is the sample size. h of A and h of S of i can be extracted from a pre-trained model, e.g., SentenceBERT.
- From Eq.(7), we can see the semantic score s(A|Q) is only dependent on the semantic feature h of A and regardless of A’s surface form.
- Therefore, our method will produce similar semantic scores for synonymous choices, assuming that the synonymous choices have similar semantic features.
Refrences
- https://arxiv.org/abs/2105.14781
Feel free to share!